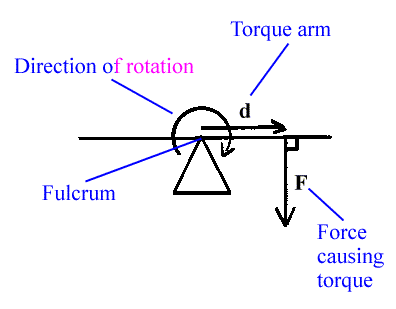
What is Torque? Torque is similar to a force, except torque is a rotational force. When we talk about force in general, we are talking about a change in linear motion. We can find torque by following:
Since r is a cross product of F, we can say:
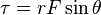
r is the distance from the point of rotation where a force is applied, F is the magnitude of the force, and θ is the angle between the force and a line from the point of rotation.
For the object to be in equilibrium, the net torque must be equal to 0, Στ = 0. So, Lmg = rFsinθ. Where L is the distance from the point of rotation to weight.
Overview:
In this lab, we are using a meter stick balanced at the center of mass of the meter stick and hanging a mass on one side, we used a meter stick, because it is easy to determine r and L. We use a force meter to determine F as we pull on the force meter to put the meter stick in equilibrium. First, we keep the force meter in a constant r spot, and change θ to see the change in F needed to put the system in equilibrium. Then, we kept θ constant and changed the r of the force meter.
Materials:
-meter stick
-force meter
-fulcrum/balance point
-mass
Data:
Data collected with graphs can be found here
I pulled the graphs so they can be analyzed easier.
Analysis:
From our first graph, we can see as sinθ gets closer to 1, the force needed to put the meter stick in equilibrium decreases. This agrees with the equation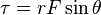. When sinθ reaches 1, we have reached the minimum force needed to put the meter stick at equilibrium. When sinθ approaches zero, we reach maximum force needed to put the meter stick in equilibrium. This is because when θ = 90, we are pulling with only a vertical force, where as, if we pull when θ = 60, now we have a horizontal and vertical force. The vertical force when θ = 60 is the same as the vertical force when θ = 90, but when we add the horizontal force, we use the Pythagorean Theorem to get the actual force that we are pulling with.
From our second graph, we can see that as r, or the distance from the rotation point to the force, gets smaller, the force gets larger. This is because as we get closer to the point of rotation its tougher to rotate the object. Imagine if I were to pull right next to the point of rotation. This is practically pulling at the point of rotation, so the meter stick won't be in equilibrium and not even close.
I work at a furniture store and sometimes we have to build furniture using the allen wrench provided for us. (The spaces are too small to get a drill into). Here is a picture of an allen wrench:
If I were stick the long end into the bolt, as the bolt tightens, if becomes nearly impossible to completely tighten the bolt. This is because the distance from the turning point to the force is really small. It doesn't matter how long I make the allen wrench if my "r" is still the same. When I turn the allen wrench the other way, the short end is now sticking out from the bolt, I can completely tighten the bolt. My torque is much bigger than before because my distance from the turning point is much greater.
Here is a numerical calculation to show this application is true:
Let's say I need a torque of 200N to completely tighten the bolt. If I use the short end to turn the bolt my r is 10cm. The maximum force that I can apply to the short end of the allen wrench is only 1500N. My torque is only 150N and I cannot completely tighten the bolt. However, I use the long end of the allen wrench my r becomes 50cm and my maximum force is still 1500N. Now, my new torque is 750N, which is more than enough to tighten the bolt, in fact, I would probably strip the bolt with this amount of force.
From our first graph, we can see as sinθ gets closer to 1, the force needed to put the meter stick in equilibrium decreases. This agrees with the equation
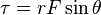. When sinθ reaches 1, we have reached the minimum force needed to put the meter stick at equilibrium. When sinθ approaches zero, we reach maximum force needed to put the meter stick in equilibrium. This is because when θ = 90, we are pulling with only a vertical force, where as, if we pull when θ = 60, now we have a horizontal and vertical force. The vertical force when θ = 60 is the same as the vertical force when θ = 90, but when we add the horizontal force, we use the Pythagorean Theorem to get the actual force that we are pulling with.From our second graph, we can see that as r, or the distance from the rotation point to the force, gets smaller, the force gets larger. This is because as we get closer to the point of rotation its tougher to rotate the object. Imagine if I were to pull right next to the point of rotation. This is practically pulling at the point of rotation, so the meter stick won't be in equilibrium and not even close.
I work at a furniture store and sometimes we have to build furniture using the allen wrench provided for us. (The spaces are too small to get a drill into). Here is a picture of an allen wrench:
If I were stick the long end into the bolt, as the bolt tightens, if becomes nearly impossible to completely tighten the bolt. This is because the distance from the turning point to the force is really small. It doesn't matter how long I make the allen wrench if my "r" is still the same. When I turn the allen wrench the other way, the short end is now sticking out from the bolt, I can completely tighten the bolt. My torque is much bigger than before because my distance from the turning point is much greater.
Here is a numerical calculation to show this application is true:
Let's say I need a torque of 200N to completely tighten the bolt. If I use the short end to turn the bolt my r is 10cm. The maximum force that I can apply to the short end of the allen wrench is only 1500N. My torque is only 150N and I cannot completely tighten the bolt. However, I use the long end of the allen wrench my r becomes 50cm and my maximum force is still 1500N. Now, my new torque is 750N, which is more than enough to tighten the bolt, in fact, I would probably strip the bolt with this amount of force.
